4탄 추측과 정당화, 수능 12번 (부모의 마음을 가진 평가원)
[추측과 정당화 (feat. Route Finding)]

2024학년도 수능 12번
1) 문제에서 묻는 것은 "g(x)와 x축으로 둘러싸인 영역의 넓이"의 최댓값이다.
2) 그렇다면 g(x)는 무엇인가? 주어진 정보를 보니, 삼차 함수 곡선과 그 위의 한 점을 지나는 기울기가 -1일 직선으로 이루어져 있다.
(여기서 중요한 것은 기울기가 -1이면서 점 (t, f(t))를 지나는 직선의 표현을 이해하고 있어야 한다, 참고로 그런 의미를 갖고 있다면 의미에 맞게 표현을 준다. 그리고 잘 이해하고 있다면 생각하지 않아도 그렇게 읽힌다. 직선을 표현 하면서는 절대 f(t)-(x-t)와 같이 주지 않는다는 것이다. 231122의 (가)조건을 직선으로 해석되지 않는 이유도 그렇다...)

231122(가) 조건 - 참고용
3) 이때 t의 위치에 따라 넓이가 달라짐을 이해했을때 기울기가 -1인 접선에서 최댓값을 갖는다는 추측을 할 수 있는데... 확실한가?
그렇지 않다. 이 문제에서 아주 운좋게 됐을 뿐이고, 그런 학생도 맞출 수 있도록 함수를 만들어 준것이다. 출제 의도도 이런 추측을 할 수 있는가에 대해 묻는 것일 것이다. 따라서 문제를 푸는 시험장에서는 이렇게 푸는 것이다.
평가원은 언제나 부모의 마음(제발 맞혀줘...)으로 출제한다. 그런데 서술형이거나 논술 문제로 나왔다면 정당화 과정을 거치지 않을 경우 감점일 것이고, 문제를 해설하는 사람이라면 이런 이야기는 해줘야하는것 아닌가....? 이제 이 문제를 통해 다른 문제를 맞혀야하는데...
사실 수학2의 고려 대상이 아닌 변곡점이 0과 6사이에 있고 이 변곡점에서의 기울기가 -1이면... 그보다 x좌표가 가장 큰 지점에서...최댓값을 갖게 된다. 하지만 이런것을 학생에게 요구하는 것이 아니다.따라서 6을 t범위에서 빼준 것이고, 또한 답이 되는 접선의 방정식이 (9,0)을 지나기도 하기에 정확하게 정당화 과정을 거치지 않고 답을 맞출 수 있긴 할 것이다.
4) 즉, 3탄에서 이야기 했던 맞힌 문제를 소재로 공부한다는 의미로 우리는 '추측을 정당화' 해보려고 한다. (언제나 이 문제를 맞히기 위한 것이 아니라 이 문제를 통해 앞으로 나올 문제를 맞춰야 하기 때문이다) 그렇다면 어떻게 정당화 했는가? 문제에서 f(x)를 인수분해 해서 주었으므로 근을 가지고 그래프를 그리고 기울기가 -1인 직선을 긋는다. 아주 운이 좋다면 그림으로 바로 풀렸을 것이다. (느낌으로 알았겠지만 '유클리드 5번 공리인 부분은 전체보다 항상 작다'로 정당화했다면...) 묻는 것을 이제 식으로 나타내보자.

이것을 미분하여 최댓값을 찾아 정당화 한다.

5) 이후에 연산이다.
1탄 [글의 시작 - 묻는 것에 따라 어떻게 계획하고 행동을 할 것인가 생각하자]
2탄 [해설지가 뭐 이래...? 해설이 아니라 계산지 아닌가....? (feat. 수능 13번)]
3탄 [수능 5번, 맞힌 문제로 공부하기]
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.





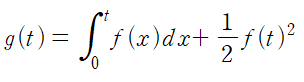
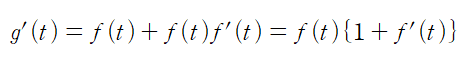














수학 100점을 목표로 하고 있는데 수놀음님으로 수학에서 새로운 깨달음을 얻어서 감사합니다.. 제가 기출분석을 하면서 231122는 어떻게 분석해야 할지를 정말 모르겠는데 수놀음님의 관점으로 알고 싶은데 유튜브에 올라갈 예정 있으신가요?
이런 댓글이 있었군요... 수도 없이 수업했던 내용인데 다음 수업 때 한번 찍어서 올려보겠습니다.