명제파트 수능 기출문제 질문
98수능 12번 문항인데요, 문제에서 p를 만족하는 q가 존재하다 형식의 명제가 있습니다.
그리고 보기에는 그 명제를 귀류법으로 증명 하는것 같은데요.
근데 귀류법이라는게 명제를 가정과 결론으로 나눈 상태에서 결론을 부정해서 참이라 보고
연역적으로 추론해서 모순을 발견해서 결과적으로 부정하기 이전의 명제가 참임을 증명하는 방법으로 알
고 있는데요,
1. p를 만족하는 q가 존재한다의 명제에서 q가 가정이고 p가 결론인가요?
2. 만약 그렇다면 위 보기의 증명과정에서 도출되는 참인 명제는 m,n이 정수이면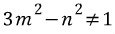 
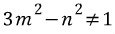이다
이다 인데....(보기에서 m,n을 정수라 가정함)
왜 문제에서 주어진 명제는 3m^-n^=1을 만족하는 m,n이 모두 정수인 해는 없다로 표현 되나요?
(이 명제는 m,n이 정수이면 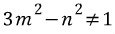이다의 '이' 인데요..)
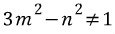이다의 '이' 인데요..)0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
[배경지식]
p →q를 부정하면 p and ~q가 됩니다.
예를 들어서
(p)국회의원은 (q)정신병자다.
라는 명제를 부정하고 싶다면
(p)국회의원이면서 (~q)정신병자가 아닌 경우를 찾아내면 돼요.
귀류법이란
p and ~q를 가정하고 모순을 이끌어내는 논증의 기술입니다.
모순의 모양이 어떠해야 한다고 단정지어 말할 수는 없어요.
p and ~p일수도 있고, q and ~q일수도 있고
어떤 방식이건 모순을 이끌어내면 되는데요.
반면 대우증명법은
p→q를 증명하기 위해서
~q라 가정하고 ~p를 이끌어내는 방법을 의미합니다.
질문자는 대우증명법과 귀류법을 좀 믹스해서 이해하고 있네요.
[질문1에 대한 답변]
구조를 분석하기 위해서 다음과 같이 기호를 붙여보겠습니다.
(p) 3m²-n²=1
(q) 정수순서쌍(m,n)
이제 문제에서 증명하고자 하는 명제는
(p and q)는 존재하지 않는다.
로 표현할 수 있습니다. 조건문(→)이 아니라 and로 두 조건이 서로 연결되어 있다는 점을 주의해야겠지요.
[질문2에 대한 답변]
제시문에서는 주어진 명제를 증명하기 위해서
p and q를 가정하고 모순(0 = 1 or 2 )을 이끌어내고 있습니다.
앞서 간단히 언급한 것처럼
질문자는 and로 연결된 부분을 조건문(→)으로 이해해서 혼란을 느끼고 있네요.
상세한 답변 고맙습니다..이해가 잘 되네요.